Les systèmes oscillants
1 Classification expérimentale des oscillateurs et propriétés
1.1 Classification expérimentale des oscillateurs
Oscillateur libre non amorti.
L'oscillateur libre non amorti, quelle que soit sa nature particulière (pendule simple, composé ou élastique, balancier de montre à ressort spiral) est caractérisé par la constance de l'amplitude de ses mouvements une fois qu'il a été lancé. De plus, la période des petites oscillations ne dépend pas de l'amplitude des mouvements, mais seulement des caractéristiques de l'oscillateur lui-même. On dit que ses petites oscillations sont isochrones. L'oscillateur libre non amorti a une énergie mécanique constante : il est conservatif.
Oscillateur libre amorti.
L'amplitude des oscillations s'atténue. La durée d'un aller-retour est constante, mais n'a pas tout à fait la même valeur que la période des oscillations de l'oscillateur libre non amorti. Cela est caractéristique d'un oscillateur libre amorti. L'oscillateur libre amorti a une énergie mécanique décroissante : il est dissipatif.
Oscillateur auto-entretenu.
On peut vérifier expérimentalement que la période de l'oscillateur auto-entretenu s'identifie à celle, idéale, de l'oscillateur correspondant libre non amorti qui n'existe que de façon temporaire.
Oscillateur forcé.
Pour un oscillateur forcé, en régime permanent, la période d'oscillation ne dépend plus du tout des caractéristiques propres de l'oscillateur (la masse m, la raideur k du ressort d'un pendule élastique). Elle est imposée par l'action extérieure de l'excitateur.
1.2 Propriétés caractéristiques des oscillations
La fréquence d'oscillation f est égale au nombre d'allers et retours par seconde. Elle est lié
à la période T de l'oscillateur par la relation :
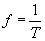
avec f en Hz (Hertz) et T en s.
Ainsi, 1 Hz = 1s-1. Le stroboscope, le périodemètre et le fréquencemètre sont des instruments usuels de détermination de la période d'un oscillateur.
2 Oscillateurs mécaniques libres non amortis
2.1 Le pendule simple
Lors de l'oscillation d'un pendule simple, libre non amorti, il y a échange entre l'énergie potentielle de pesanteur et l'énergie cinétique. La source de ces deux énergies, appelée énergie mécanique, se conserve au cours du temps.
Le mouvement du pendule simple dans le cas de petites oscillations peut être interprété en terme de mouvement au fond d'une cuvette " d'énergie potentielle ".
L'équation différentielle réglant les petites oscillations d'un pendule simple s'écrit :
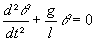
avec q (en °) l'angle entre le pendule et la verticale, t (en s) le temps, g (en m.s-2)
l'accélération de la pesanteur (g = 9, 81 m.s-2) et l (en m) la longueur du pendule.
La solution de cette équation est sinusoïdale, de période :
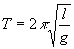
2.2 le pendule élastique horizontal
Le pendule élastique horizontal, libre non amorti, est conservatif du point de vue énergétique. Son énergie potentielle élastique et son énergie cinétique s'échangent au cours du temps, mais la somme de ces énergies est invariable. Lorsque l'énergie potentielle élastique est maximale, l'énergie cinétique est minimale (et inversement).
L'équation différentielle réglant les oscillations du pendule élastique est :
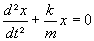
avec x (en m) la position du pendule, t (en s) le temps, k la raideur du ressort
et m (en kg) la masse accrochée au ressort.
La solution de cette équation est sinusoïdale, de période :
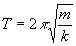
3 Oscillateurs mécaniques forcés
3.1 Le pendule de torsion en oscillations forcées
Un oscillateur amorti peut être " forcé " de façon sinusoïdale par un excitateur extérieur, à la fréquence f. Après un premier épisode transitoire, souvent complexe à analyser, l'oscillateur se place en régime sinusoïdal permanent, oscillant à la même pulsation que l'excitateur.
La grandeur oscillante et l'excitation sont alors déphasées l'une par rapport à l'autre. De plus, l'amplitude des oscillations en régime permanent dépend de la pulsation du signal délivré par l'excitateur. L'expression de l'amplitude de la grandeur oscillante, en régime sinusoïdal permanent, en fonction de la pulsation w du signal excitateur détermine la " réponse en fréquence " de l'oscillation forcée.
La courbe A(w) ou A(f), avec w = 2pf, définit l'éventuelle " résonance " de l'oscillateur. De même, le déphasage j de la grandeur oscillante par rapport à l'excitation dépend de w. j(w) constitue la réponse de phase en fréquence.
3.2 Le phénomène de résonance en amplitude d'élongation
Il est lié à l'amortissement de l'oscillateur. L'amortissement peut être si fort que l'amortissement disparaît. A contrario, la résonance en vitesse (dérivée de la grandeur oscillante par rapport au temps) a toujours lieu, quel que soit l'amortissement, à la pulsation d'excitation égale à celle propre de l'oscillateur. Lorsque l'amplitude des oscillations est maximale, A vaut Ar = A(wr). On dit qu'on est à la résonance en élongation (c'est de la grandeur oscillante q(t) qu'il s'agit). Ar est l'amplitude de l'élongation à la résonance. wr est appelée pulsation de résonance et fréquence de résonance.