KeepSchool > Fiches de Cours > Lycée > Physique > Les oscillateurs électriques - Modélisation des systèmes oscillants

Les oscillateurs électriques - Modélisation des systèmes oscillants. Fiches de Cours de Physique destinée aux élèves de Lycée.

Primaire

Collège

Lycée

Les oscillateurs électriques - Modélisation des systèmes oscillants

1 Oscillations libres d'un circuit LC

Au cours des oscillations dans un circuit LC, il y a transfert d’énergie entre le condensateur et la bobine. La somme des énergies emmagasinées par le condensateur et la bobine à une date t est constante :

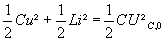
UC, 0 représente la tension aux bornes du condensateur chargé.

Un circuit LC isolé électriquement, qui possède de l’énergie électromagnétique, est le siège d’oscillations libres. Elles sont sinusoïdales. Au cours des oscillations libres d’un circuit LC, il y a conversion de l’énergie électrique emmagasinée par le condensateur en énergie magnétique emmagasinée par la bobine, et réciproquement. Dans un circuit LC isolé électriquement, on a :
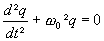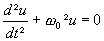et avec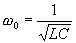

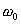est appelée pulsation propre du circuit.

Pendant les oscillations libres d’un circuit LC, le condensateur étant initialement chargé, on peut écrire :

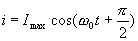
La période propre d’un circuit LC est :

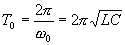
2 Oscillations d'un circuit RLC

2.1 Entretien des oscillations d'un circuit RLC

Le régime d’oscillation d’un circuit RLC dépend de la valeur de R :

• Si R = 0, les oscillations sont libres non amorties de période T₀
• Si R < RC (valeur critique de R), les oscillations sont libres et amorties de pseudo-période T₀
• Si R = RC, le régime est apériodique
• Si R > RC, le régime est apériodique surcritique. Dans ces deux derniers cas, il n’y a plus d’oscillations.

Dans un circuit RLC isolé électriquement, on a :
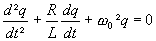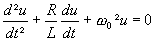et avec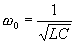

2.2 Oscillations forcées d'un circuit RLC

Observation et équations

Un dipôle RLC monté en série avec un générateur GBF oscille à la fréquence de la tension excitatrice : il est le siège d’oscillations forcées.

L’impédance d’un dipôle est définie par :

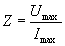L’impédance dépend de la pulsation.

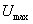désigne l’amplitude de la tension aux bornes de l’association RLC et 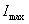l’amplitude de l’intensité traversant cette association.

L’équation différentielle d’un circuit RLC en régime sinusoïdal forcé est :

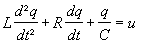
Résonance d’intensité

A la résonance, la pulsation w de la tension excitatrice est égale à la pulsation propre 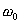du circuit :

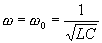
A la résonance, Z = R et il y a un risque de surtension aux bornes du condensateur et de la bobine.

Bande passante

La largeur 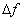de la bande passante à 3dB est :

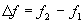
où f2 et f1 désignent les fréquences pour lesquelles :

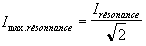
Facteur de qualité du circuit

Le facteur de qualité est égal au rapport entre la fréquence de résonance et la largeur de la bande passante à 3dB :

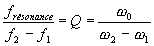
3 Modélisation des systèmes oscillants

3.1 Analogie oscillateur mécanique-oscillateur électrique

Les équations qui règlent le mouvement d’un pendule élastique et la charge d’un condensateur dans un circuit RLC série sont formellement analogues. On peut passer de l’une à l’autre par simple transposition de notations. Dans les deux cas, on peut mettre en évidence la pulsation propre et le facteur qualité :
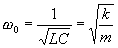et

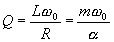
L’analyse dimensionnelle des différents termes des équations différentielles permet d’éviter de grossières erreurs d’inhomogénéité.

Dans un circuit RLC série, l’énergie électrique ne se conserve pas au cours du temps ; elle se dissipe par effet Joule dans la résistance. De la même façon, l’énergie mécanique d’un oscillateur élastique amorti n’est pas conservée ; elle est dissipée par frottements de type fluide visqueux. Des oscillations électriques ou mécaniques s’amortissent de ce fait. Si l’on veut entretenir les oscillations, il faut un apport constant d’énergie pour compenser les pertes.

3.2 Amorçage et stabilisation d'oscillations

Amorçage des oscillations créées dans un montage à résistance négative

L’utilisation d’un circuit à amplificateur opérationnel permet de simuler un dipôle à résistance négative obéissant à la loi d’Ohm : 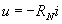La résistance négative est l’élément capital qui permet d’entretenir, par apport d’énergie extérieure les oscillations d’un système physique qui, sans elle, s’amortiraient inévitablement. La stabilisation des oscillations amorcées par une résistance négative exige dans le système des éléments non linéaires.

Modèle non linéaire de Van der Pol et sa simulation informatique

Dans le cas de simulation de résistance par un circuit à amplificateur opérationnel, c’est le phénomène de saturation en tension de sortie qui assure la non-linéarité indispensable à la stabilisation de l’oscillateur. Le circuit à amplificateur opérationnel se comporte comme un puits de résistance négative : Le puits de résistance est linéaire par morceaux.

Van der Pol a eu l’idée d’approcher le puits de résistance linéaire par morceaux, par une fonction parabolique. On aboutit à l’équation différentielle canonique de Van der Pol :

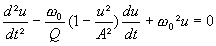
avec

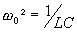
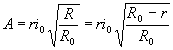
Selon le signe de, on disposera dans l’équation de Van der Pol d’un terme de résistance positive ou négative. Cette alternance de comportement assure la stabilisation des oscillations.

L’équation canonique de Van der Pol n’a pas de solution analytique simple. Le calcul numérique sur ordinateur, par sa rapidité et sa puissance, permet une visualisation commode de la solution de l’équation de Van der Pol. On constate de visu les phases d’amorçage, d’amplification et de stabilisation des oscillations quasi sinusoïdales en régime permanent. En pratique, le démarrage des oscillations exige des conditions particulières définissant la plage d’accrochage de l’oscillateur. Lorsque la condition d’amorçage est juste satisfaite, les oscillations créées sont pratiquement sinusoïdales. Si on dépasse franchement les conditions d’accrochage, les oscillations stabilisées prennent un caractère rectangulaire : on a fabriqué un oscillateur de relaxation.