Généralités sur les fonctions
1 Fonction et courbe représentative
Définition 1 :
Soit I un intervalle ou une réunion d'intervalle de R.
Définir une fonction f de I dans R, c'est associer à chaque réel x de I au plus un réel de R noté f(x).
I est alors l'ensemble de définition de f : on dit que f est définie sur I
f(x) est ainsi un réel qui est l'image de x par f.
Définition 2 :
Le graphique qui réunit tous les points M de coordonnées ( x, f(x) ) où x décrit l'ensemble de définition I de f est la courbe représentative de f dans un plan. L'ensemble des x décrit l'ensemble de définition de f. On a l'habitude de le noter I ou D.
Remarques :
- Pour représenter cette courbe représentative de f, on utilise un tableau de valeurs.
- Les unités ne sont obligatoirement pas les mêmes sur les deux axes.
- Le tracé de la courbe représentative d'une fonction ne peut jamais être exacte, d'autant plus que l'on est limité matériellement par la feuille de papier. ( il est impossible de tracer une courbe jusqu'à +¥ par exemple)
Exemple de graphique de fonction
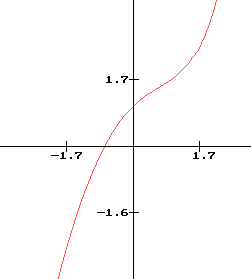
2 Variations d'une fonction
Définition 1 :
Soit une fonction f définie sur un intervalle I, soit a et b deux éléments de I tels que a < b.
- f est croissante (respectivement strictement croissante)sur I si et seulement si f(a) £ f(b) (respectivement si f(a) < f(b)).
- f est décroissante sur I (respectivement strictement décroissante) si et seulement si f(a) ³ f(b) (respectivement si f(a) > f(b)).
Remarque : la distinction entre inégalité stricte et large est fondamentale ici pour bien distinguer une fonction croissante (ou décroissante) d’une fonction strictement croissante (ou décroissante). En effet, une fonction croissante et non strictement croissante peut être constante.
Conclusion : étudier le sens de variation d’une fonction, c’est donc déterminer, lorsqu’ils existent, les plus grands intervalles sur lesquels cette fonction est croissante ou décroissante.
Définition 2 :
Soit une fonction définie sur un intervalle J . f est monotone sur J si et seulement si f est croissante ou décroissante sur J en entier.
Le tableau de variation d’une fonction rassemble les données et les propriétés d’une fonction. En particulier, il fait apparaître
- l’ensemble de définition de la fonction
- la parité de la fonction (cf plus bas)
- les variations de la fonction (croissance, décroissance )
- les valeurs remarquables de la fonction
Soit f une fonction définie sur [-4 ; 4], paire, croissante sur [-4 ; 4], avec f(0) = 6 et f(-4) = f(4) = -1
On va résumer l’ensemble de ces informations dans le tableau de variation de f
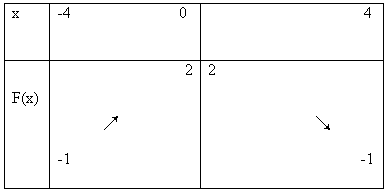
3 Parité
3.1 Fonctions paires
Définition : une fonction est paire si et seulement si :
- son ensemble de définition I est symétrique par rapport à 0
- pour tout x de I, on a f(-x) = f(x)
Représentation graphique : la courbe représentative d'une fonction paire dans un repère orthogonal est symétrique par rapport à l'axe des ordonnées.
Exemple d'une fonction paire : la fonction valeur absolue que l'on notera f
- f est définie sur R ( ]-¥ ; +¥[ ). R est donc bien symétrique par rapport à 0
- pour tout x de R, f(-x) = |-x| = |x| = f(x)
3.2 Fonctions impaires
Fonctions impaires
Définition : une fonction est impaire si et seulement si :
- son ensemble de définition I est symétrique par rapport à 0
- pour tout x de I, on a f(-x) = -f(x)
Représentation graphique : la courbe représentative d'une fonction impaire dans un repère orthogonal est symétrique par rapport à l'origine du repère du plan.
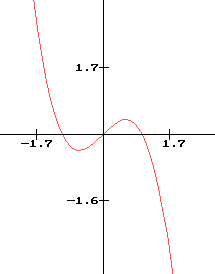
Exemple d'une fonction impaire : la fonction g définie sur J = [ -5 ; 5 ] par g(x) = x^3 - x
- L'ensemble de définition [ -5 ; 5 ] est bien symétrique par rapport à 0
- pour tout x de J, on a g(-x) = (-x)^3 - (-x) = -x^3 + x = -g(x)
Graphique de la fonction g
4 Maximum et minimum d'une fonction
Définition : soit f une fonction dont l'ensemble de définition est D et I un intervalle de D.
- On dit que f admet un maximum en a sur I si, pour tout x de I : f(x) £ f(a). f(a) est ce maximum.
- On dit que f admet un minimum en b sur I tel que, si pour tout x de I : f(x) ³ f(b). f(b) est ce minimum.