Angles de vecteurs et fonctions circulaires

1 Les radians

Rapport entre degrés et radians

Le radian est une unité de mesure des angles. En radians, l'angle plat mesure p. (p est un nombre dont la valeur est égale à 3, 14 environ). On a donc p = 180°.

Remarques :

l'abréviation de " radian " est souvent " rad ".
La mesure d'un angle en radians peut être effectuée à l'aide d'un rapporteur.

On a les correspondances suivantes :

Degrés	Radians
0	0
30	p/6
45	p/4
60	p/3
90	p/2
180	p

D'une manière générale, si un angle DÊF a comme mesure en degrés m, et en radians M, alors on a : m/180 = M/p.

Longueur d'une arc de cercle :

Définition : Soit C un cercle de centre O et de rayon r, et A et B deux points sur ce cercle. Soit L la longueur de l'arc de cercle AB, et M la mesure en radians de l'arc de cercle AÔB. On a alors : L = Mr

Remarque : quand r = 1, la longueur de l'arc de cercle est égale à sa mesure en radians.

2 Orientation du plan et arcs

Deux sens de parcours sont possibles dans un cercle (le sens des aiguilles d'une montre, ou le sens inverse). Orienter un cercle revient à en choisir un. L'orientation choisie par les mathématiciens est le sens trigonométrique, qui est le sens inverse des aiguilles d'une montre. (appelé également le sens direct).

Cercle trigonométrique :

Un cercle de rayon égal à 1 et orienté dans le sens trigonométrique est appelé nommé cercle trigonométrique.

Définition: Soit C un cercle trigonométrique. On note 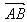(en incurvant légèrement la flèche) un arc de cercle trigonométrique défini par deux points A et B situés sur C

Si L est une mesure d'un arc orienté, il suffit d' ajouter 2p à L pour obtenir une autre mesure de cet arc. Plus généralement, il suffit d'ajouter 2np (où n est un entier).

Théorème : Un arc orienté 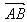de cercle trigonométrique C a une mesure et une seule qui appartienne à l'intervalle ]-p;+p[. On appelle cette mesure la mesure principale de l' arc.

Important : Soit 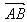un arc. Sa mesure est l'opposé de celle de l'arc.

Théorème : Soient P, Q et R trois points d'un cercle trigonométrique C. Une mesure de l'arc 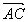est la somme d'une mesure de 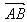et d'une mesure de. (moyen mémotechnique : ce théorème peut s'apparenter à la relation de Chasles appliquée aux arcs de cercle).(cf fiche sur les vecteurs).

3 Angles orientés

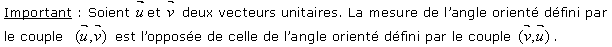
Propriétés : Deux angles définissent le même angle orienté de vecteurs unitaires lorsque leurs arcs respectifs ont le même ensemble de mesures. Un unique angle de vecteurs unitaires admet pour mesure un réel r fixé.

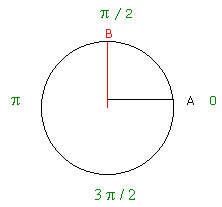
Point M de C associé à un réel x :

Définition : Soit C un cercle trigonométrique de centre O et A un point fixe sur C. On dit que le point M de C est associé au réel x, si x est une mesure en radians de l'angle orienté de vecteurs.
Exemple : Le point B est associé au réel p / 2

4 Fonctions sinus et cosinus

Définitions :

x est un réel quelconque;
D est le point du cercle trigonométrique associé à x.
Le cosinus de x (noté cos x )est l'abscisse de M dans le repère R;
Le sinus de x (noté sin x) est l'ordonnée de M dans le repère R.

Propriétés :

soit x un réel quelconque. Alors
-1 £ cos x £ 1 et -1 £ sin x £ 1.
De plus, on a : cos²x + sin²x = 1

Propriétés des fonctions cos et sin.

a) Fonction cosinus.

La fonction cos est strictement décroissante sur [0 ; p ]. Comme elle est paire, elle est décroissante sur [p;2p].
Elle atteint son maximum en 0, ce maximum étant 1.

b) Fonction sinus

La fonction sin est strictement croissante sur [0 ; p / 2] et strictement décroissante sur [ p / 2 ; p].
Elle atteint son maximum en p / 2, ce maximum étant 1.

Valeurs remarquables :

x (en radians)	0	p/6	p/4	p/3	p/2
cos x	1	V3/2	V2/2	1/2	0
sin x	0	1/2	V2/2	V3/2	1

Définition : Soit f une fonction définie sur R et k un réel strictement positif. La fonction f est périodique de période k si, pour tout réel x, f (x + k) =f (x).

Important : les fonctions sinus et cosinus sont des fonctions périodiques de période 2p.

5 Formulaire de trigonométrie

x désigne un réel quelconque

cos (-x) = cos x
sin (-x) = sin x

Remarque : Si A est le point associé à x sur un cercle trigonométrique C, alors A', associé à -x est son symétrique par rapport à l'axe des abscisses.

cos ( x + p) = - cos x
sin (x + p) = - sin x
cos ( p - x) = - cos x
sin ( p - x) = sin x
cos ( x - p/2) = sin x
sin ( x - p/2) = cos x
cos (x + p/2) = - sin x
sin (x + p/2) = cos x.

Définition :

Fonction tangente : Pour tout réel x tel que cos x est non nul, on appelle tangente de x (noté tan x) le réel

tan x = (sin x) / (cos x).

KeepSchool > Fiches de Cours > Lycée > Maths > Angles de vecteurs et fonctions circulaires